Software
The GAGE Facility (GAGE) promotes research and learning in geodesy by providing a variety of software, including web applications, and desktop utilities for scientists, instructors, students, and others. Web-based data visualization and mapping tools provide users with the ability to view post–processed data while web-based geodetic utilities provide ancillary information. Downloadable stand-alone software utilities include applications for performing computations on raw data, e.g., data pre-processing and post-processing, and data management tasks, and geodetic modeling. Get help with issues related to the Software section of our site.
For various pre-processing or post-processing of GPS/GNSS and TLS data:
- TEQC (Translation, Editing and Quality Checking) — GPS/GNSS format translating, correct GPS/GNSS metadata, time window or perform other filtering, and/or GPS/GNSS quality check.
- GPS/GNSS Pre-processing Tools — Hatanaka, Trimble's runpkr00, and other pre-processing tools for various tasks
- GPS/GNSS Post-processing Tools:
- TLS Software — community access to a variety of LiDAR and geospatial software packages.
- SAR Software — community access to a variety of SAR processing packages, maintained by GAGE on the WiSAR site.
Data management sofware subsystems for regional geodesy data managers are available.
- GSAC — Geodetic Seamless Archive Center, a free, open-source software package that provides web services for discovery, sharing, and access to geodetic data and metadata associated with site-located instruments.
- Dataworks for GNSS is a project to provide a turnkey system for regional GNSS data management of small networks which is being developed in stages as subsystems, e.g. one subsystem component being GSAC.
To assist all levels of users, visualization and mapping tools are available through GAGE. These applications and notebooks allow users to display data for individual or small groups of data points in a variety of ways.
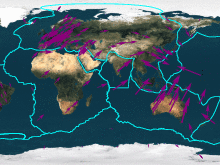
- GPS Velocity Viewer allows exploration of PBO-site geodetic plate velocities, or your own geodetic velocities, in various reference frames.
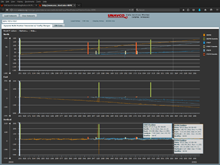
- Time series plotting tools allow users to see and analyze data temporally.
- Interactive GNSS Position Timeseries Plotter dynamically plots North, East, and Vertical GPS/GNSS positions over time and optionally provides site maintenance event information.
- GNSS Position Timeseries Plotter Notebook (edit URL parameters to change station ID and dates).
Geodetic utilities provide supporting information associated with geodetic positioning.
- Plate motion calculator calculates rigid plate motions at one or more specified locations on Earth using one or more plate motion models.
- Geoid height calculator calculates a geoid height correction at one or more specified locations on Earth using the EGM96 gravity model.
Last modified: 2024-05-24 17:45:13 America/Denver
)