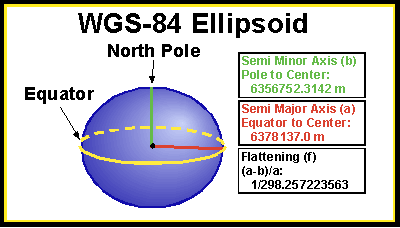
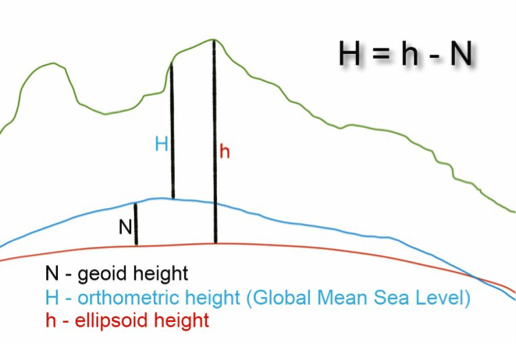
These tutorials are designed for students and the general public to introduce key concepts in the Global Positioning System (GPS), the United States component of the Global Navigation Satellite System (GNSS). Learn about reference ellipsoids and the geoid, the advantages of using models in science, and how a GPS receiver determines elevation.